Found on the project by Bryan. Congratulations.

[Alez]

Early morning of 15 December 2017 with 2 hours and 22 minutes difference, project server received two results for workunit R9_000478253 - from damotbe (L'Alliance Francophone) and Bryan (SETI.USA). Both files are identical (as it must be for correct results) and contain an 8 squares. Many of computation results contain 8 and even more squares, but is this case only first two of them corresponds to usual pair of ODLS, but other 6 squares... were mutually orthogonal! (And, of course, all of this squares were constructed by rows permutation!)

We get a first of squares from this MODLS set and found all (not only "permutation") orthogonal diagonal Latin squares for it, then - all ODLS for "root square" and the squares, found on the previous step, and repeat this process until while we were given a new squares. The results of this search you can see in figure below.

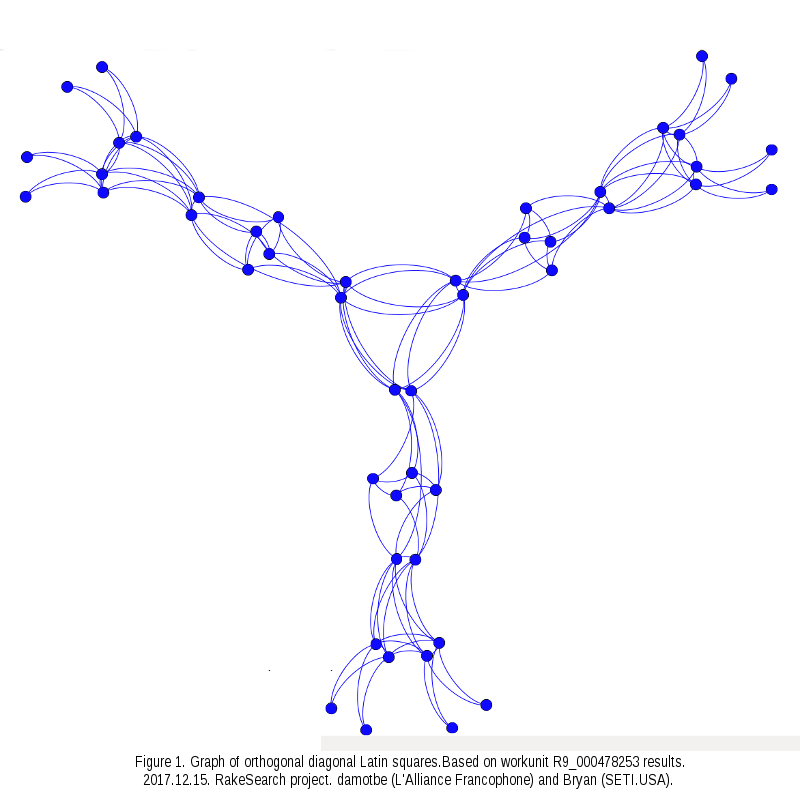
Squares, presented in this graph as nodes and edges denote an orthogonal relationship between squares, lined up into astonishing, symmetrical figure! The core of it is fastened by six MODLS, which are broken into three groups. Each group (originating from two squares) is the basis for four-level branch constructed from 14 squares.

If you are interested in this, you can download this set of 48 squares..

[scole of TSBT]

That's one of them mimic critters from Edge of Tomorrow...

[Bryan]

Sure looks like it is the same species