![[ TSBT's Pirate ]](./images/ranks/British Army Ranks/Small Ranks/17_General.gif "[ TSBT's Pirate ]")
Welcome to the Wieferich and Wall-Sun-Sun Prime Search
A Wall–Sun–Sun (or Fibonacci–Wieferich) prime is a prime p > 5 in which p^2 divides the Fibonacci number
, where the Legendre symbol 
is defined as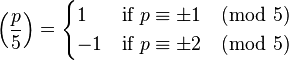 
They are named after Donald Dines Wall and twin brothers Zhi-Hong Sun and Zhi-Wei Sun. Drawing on Wall's work, in 1992 the brothers proved that if the first case of Fermat's last theorem was false for a certain prime p, then that p would have to be a Wall–Sun–Sun prime.
Although it has been conjectured that infinitely many exist, there are no known Wall–Sun–Sun primes. As of December 2011, if any exist, they must be > 9.7e14. The PRPNet search began here, and the BOINC search will as well for double-checking purposes.
The lack of success has lead to an interest in "Near" Wall-Sun_Sun primes. They are defined as special instances (with small |A|) of F_(p-(p/5)) = Ap (mod p^2).
A prime p is a Wieferich prime if p^2 divides 2^(p-1) - 1. They are named after Arthur Wieferich who in 1909 proved that if the first case of Fermat’s last theorem is false for the exponent p, then p satisfies the criteria a^(p-1) = 1 (mod p^2) for a=2.
Notice the similarity in the expression p^2 divides 2^(p-1) - 1 to the special case of Fermat's little theorem p divides 2^(p-1) - 1.
Despite a number of extensive searches, the only known Wieferich primes to date are 1093 and 3511. The rarity of these primes has lead to an interest in "Near" Wieferich primes. They are defined as special instances (with small |A|) of 2^((p−1)/2) ≡ ±1 + Ap (mod p^2).
rapper giving badges( I started hunting them, lol)